L04-高级类特性1
面向对象特征之二:继承
为什么要有继承 多个类中存在相同属性和行为时,将这些内容抽取到单独一个类中,那么多个类无需再定义这些属性和行为,只要继承那个类即可。
此处的多个类称为子类,单独的这个类称为父类(基类或超类)。可以理解为:“子类 is a 父类”
类继承语法规则:
class Subclass extends Superclass{ }
作用
继承的出现提高了代码的复用性。
继承的出现让类与类之间产生了关系,提供了多态的前提。
不要仅为了获取其他类中某个功能而去继承。
继承的规则说明
子类继承了父类,就继承了父类的方法和属性。
在子类中,可以使用父类中定义的方法和属性,也可以创建新的数据和方法。
在Java 中,继承的关键字用的是“extends”,即子类不是父类的子集,而是对父类的“扩展”。
规则
子类不能直接访问父类中私有的(private)的成员变量和方法。
Java只支持单继承,不允许多重继承
一个子类只能有一个父类
一个父类可以派生出多个子类
class Sub ...
L03-面向对象编程
面向对象与面向过程面向对象(OOP)与面向过程
二者都是一种思想,面向对象是相对于面向过程而言的。面向过程,强调的是功能行为。面向对象,将功能封装进对象,强调具备了功能的对象。
面向对象更加强调运用人类在日常的思维逻辑中采用的思想方法与原则,如抽象、分类、继承、聚合、多态等。
面向对象的三大特征
封装 (Encapsulation)
继承 (Inheritance)
多态 (Polymorphism)
类与对象类与类之间的关系
关联关系
继承关系
聚合关系
聚集
组合
面向对象思想
程序员从执行者转化成了指挥者。
完成需求时:
先去找具有所需功能的对象来用。
如果该对象不存在,那么创建一个具有所需功能的对象。
这样简化开发并提高复用。
类(class)和对象(object)是面向对象的核心概念。
类是对一类事物描述,是抽象的、概念上的定义
对象是实际存在的该类事物的每个个体,因而也称实例(instance)。
“万事万物皆对象”
java类及类的成员
现实世界万事万物是由分子、原子构成的。同理,Java代码世界是由诸 ...
L02-基本语法
关键字关键字
定义:被Java语言赋予了特殊含义,用做专门用途的字符串(单词)
特点:关键字中所有字母都为小写
保留字
Java保留字:现有Java版本尚未使用,但以后版本可能会作为关键字使用。自己命名标记符时要避免使用这些保留字。
byValue、cast、future、 generic、 inner、 operator、 outer、 rest、 var 、 goto 、const
标识符
标识符
Java 对各种变量、方法和类等要素命名时使用的字符序列称为标识符
凡是自己可以起名字的地方都叫标识符
定义合法标识符规则
由26个英文字母大小写,0-9 ,_或$组成
数字不可以开头
不可以使用关键字和保留字,但能包含关键字和保留字
Java中严格区分大小写,长度无限制
标识符不能包含空格
注意:在起名字时,为了提高阅读性,要尽量有意义,“见名知意”。
Java中的名称命名规范
包名:多单词组成时所有字母都小写:xxxyyyzzz
类名、接口名:多单词组成时,所有单词的首字母大写:XxxYyyZzz
变量名、方法名:多单词组成时,第一个单词首字母小写, ...
L01-Java语言概述
基础常识软件开发 软件,即一系列按照特定顺序组织的计算机数据和指令的集合。有系统软件和应用软件之分。
人机交互方式图形化界面 Graphical User Interface GUI,这种方式简单直观,使用者易于接受,容易上手操作。
命令行方式 Command Line Interface CLI,需要有一个控制台,输入特定的指令,让计算机完成一些操作。较为麻烦,需要记录住一些命令。
常用的DOS命令
ls:列出文件
cd:切换目录
cp:复制
mv:移动
rm:删除
mkdir:创建文件夹
chown:更改所有者
chmod:更改文件的权限
tar:打包、压缩、解压
cat:打印文件内容
ps:查看进程
kill:杀死进程
pwd:显示工作目录
计算机语言语言 是人与人之间用于沟通的一种方式。例如:中国人与中国人用普通话沟通。而中国人要和英国人交流,就要学习英语。
计算机语言 人与计算机交流的方式。如果人要与计算机交流,那么就要学习计算机语言。计算机语言有很多种,如:C,C++,Java,PHP等。
第一代 ...
L03-回归和分类
机器学习基础 机器学习主要是研究如何使计算机从给定数据中学习规律,并利用学习到的规律(模型)来对未知或无法观测的数据进行预测。
学习方式
监督学习:收获到了外界的知识
无监督学习:用得最多的是“聚类”
半监督学习:既有信息输入,但又不是全部
强化学习:不断对抗
学习结果
回归
分类
强调:目前主流学习技术是监督学习,半监督学习和强化学习在通用场景下还不是特别的work
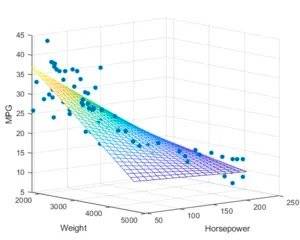
线性回归 线性回归是最基础的回归算法。
引入
思考:x与y符合什么关系呢?
观察到x与y的关系(模型选择),y=ax+b,建立线性回归模型
通过优化方法设法拟合数据,得到最优的a
评估该模型是否准确,查看训练集上的准确率
评估该模型的泛化性能,在测试集上的准确率
基本概念
训练集
测试集(交叉验证法、自助法等)
目标函数
损失函数
优化方法
拟合、过拟合、欠拟合
准确率、泛化性能
目标函数、优化方法推导 ...
L05-图论
图的由来——对现实世界的抽象哥尼斯堡七桥问题
化学研究中的分子结构表示 如,丁烷(C4H10)的两种同分异构结构用图可以表示为:
高铁线路图
期末考试时间的排布 一个学校要对期末考试进行排布,如何避免时间上的冲突?
抽象为图的模型来解决,则顶点代表待排布的课程,连接两个顶点边表示有学生同时选择了这两门课程。
问题转化为用不同的颜色去给顶点上色(顶点着色问;四色问题),要求不同时间段的考试(顶点)用不同的颜色
,相同时间段的考试(顶点)用相同的颜色。
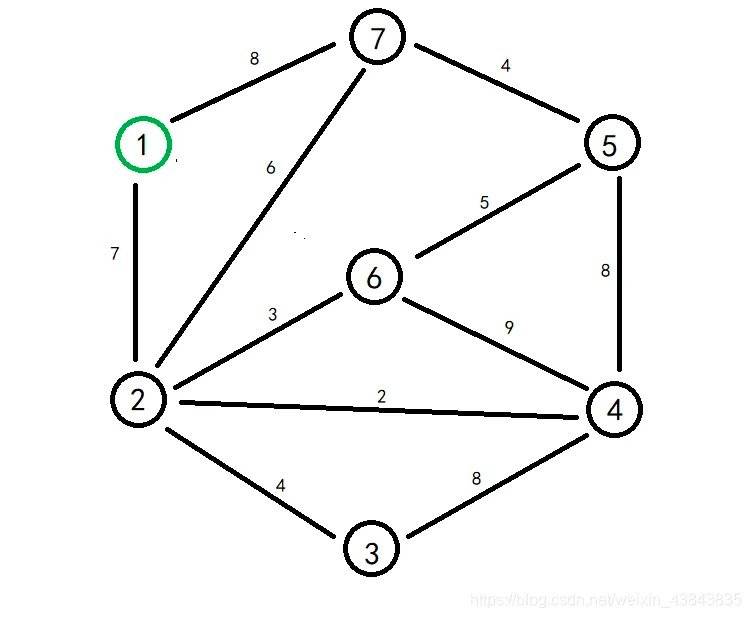
图的构成 什么构成了图:——顶点和边构成的网络结构
我们关心什么?
图中有多少个点
哪些点之间有线(边)连接
我们不关心什么?
边的长度
边是否弯曲
点的绝对位置
定义 文字定义:
一个图是一个序偶<V, E>,符号表示为: G = <V, E>
V = {v1, v2, …, vn}为有限非空集合,Vi称为顶点,或简称点,V称为顶点集,用**|V|表示顶点数**
E是有限集合,为一个图的所有 ...
L04-概率与统计
频数&频率频数 变量值中代表某特征的数的出现次数
频率 频数与总数之比
频率派视角下的概率定义 做大量重复试验时,随着试验次数的增加,某一事件出现的频率,总在一个定值的附近稳定地摆动,便将此定值称为该事件的概率。
抛硬币挑边
掷骰子猜大小
抛铜钱鼓舞士气
布丰投针试验
1、白纸上平行线间距:t
2、针的长度:l(l<t)
3、随机向纸上投针n次
4、针相交与直线的次数记为m
理论上
用X, Y分别表示针的中点到最近的平行线的距离,Y表示针与平行线的夹角,则针与直线相交的的时候,必定有:
且X在(0,t/2)内服从均匀分布,Y在(0,π/2)内服从均匀分布,XY相互独立。
则X,Y的概率密度函数为:
所以,根据用频率估计概率的原则,只要进行大量投针试验,统计出频率,就可计算出π。
总结
试验必须可以进行很多次(易于操作,成本低,周期短)
缺乏一定的严谨性(如何确定“稳定”与否)
无法对不可多次重复的事 ...
L02-人工智能中的数学基础
数学分析映射与函数
极限与连续
导数 导数是曲线的斜率,是曲线变化快慢的反应;
可导一定连续,反之不然
思考:极值如何求解?
常用函数求导公式
sigmoid 函数—模拟神经元
左边:未激活
右边:激活
导数:f’(x) = f(x) * [ 1-f(x) ]
泰勒展开
泰勒展开式
常用函数的泰勒展开
在某邻域内,存在一阶近似、二阶近似、….
逼近非线性函数求解
梯度下降
练习:使用梯度下降法求解y=x2
思考:什么情况下有全局最优解?
练习
梯度下降法:
“最快”过于盲目、有缺陷,进一步利用曲线二阶导的信息进行迭代求解,称为牛顿法
多元函数
多元函数的导数如何表达?
多元函数的梯度呢?
多元函数的二阶导是什么?
hessian矩阵G
小彩蛋Yan LeCun:可微分式编程
线性代数线性变换线性变换:指旋转、推移,他们的组合是线性变换
...
L03-线性代数
引入 今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?——孙子算经
线性方程组
由系数唯一确定
通常由高斯消元法解决
齐次线性方程组:常数项全部为0
非齐次线性方程组:常数项不全部为0
行列式 对于方阵(行数=列数)定义一种特别的运算——行列式:
如何计算:
如果阶数更高,如何计算?
全排列 n个不同元素所有不同排列方式总数:Pn=n∙(n-1)∙∙∙2∙1=n!
逆序数 对于一个排列,标准顺序规定为从小到大,大数在小数前面就称为逆序。一个排列中逆序的数目称为逆序数,用τ表示:τ(53214)=4+2+1=7
n阶行列式解法
教科书式解法:
实际上:
将矩阵转化为上(下)三角形矩阵
将高阶行列式拆分成二阶/三阶行列式
克拉默法则定义
当系数行列式不等于0时,其解唯一,且:
其中 |Ai| 就是把 |A| 中第i列元素换成常数向量,而其余各列保持不变得到的。
性质
当系数行列式不等于0时,方程组有唯一解
对于齐次线性方程组:
其有非零解的充要条 ...
L02-微积分
函数本质
从一个集合到另一个集合的映射规则
可以源于“天然”
也可以“人工”创造,如狄利克雷函数
Q:狄利克雷函数的图像应该是什么样?
客观存在,然而无法画出
表示形式
解析式:y = sinx
文字描述:自变量为无理数时因变量取值0,有理数时取值1
列表法
三要素
定义域(整数域,实数域,复数域…)
值域(整数域,实数域,复数域…)
映射法则(将定义域映射到值域)
注意!不是所有的映射法则都可以构成函数。同一个自变量,在值域中有且只能有一个因变量与之对应
极限定义
什么叫无限逼近某一个量?
这个量可以“到达”吗?
正式定义:
连续直观上
不断裂
不跳跃
处处相连
定义 设函数f(x)在点x0的某个领域内(例如(x0 - 0.0001,x0 + 0.0001))有定义,如果有:
则称函数f(x)在点x0处连续,x0称为函数f(x)的连续点。
函数在连续点的极限就是连续点的函数值!
导数定义
几何意义 函数图像上一点的导数的值为在该点切线的斜率,代表 ...