L01-数学导论
为什么需要数学
在古代,就已经有了精密的数学体系,比如沟渠的建造,算盘等。
在现代,航空工程等各方面都需要极其精密的计算。
人类如何表示数字
- 史前文明:结绳记事

- 四大文明古国:都发明了各自的文字

- 古玛雅文明:零和进位的提出

计算机可以做什么
图像处理、音频处理、模型创建、游戏······
0和1如何去做运算

二进制与十进制的转换

计算机如何处理二进制数据
- 逻辑电路

计算机为什么会产生理论上的误差
0.1+0.2=0.3,但是计算机输出的结果为:0.3000000000000004
原因:十进制小数如何转换为二进制(乘2取整法)


如何看待这个误差?
解决办法:
- 将小数扩大成整数后运算
- 提高计算机可表达数的精度
Tips:这是二进制独有的问题吗?答:并不是噢

人工智能如何运转
1、利用计算机强大的算力,按照AI模型的规则,实现特定的逻辑推断任务。
2、AI模型的建立和训练高度依存于相应的数学体系。

人工智能需要什么数学知识
微积分
线性代数
概率&统计
图论
函数

更抽象一点……
x, y,…(自变量) ⟹ f (函数) ⟹ z(因变量)
导数(一元函数)
运动问题(y:位移,x:时间)


导数定义

y被称作y′的原函数,y′被称作y的导函数(导数)
微分定义
微分:当自变量x的变化趋于无穷小时(dx),因变量f(x)的变化情况(df(x))

常用函数的导数

导数的运算法则

偏导数(多元函数)

线性代数

今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?——孙子算经

线性方程组是由什么唯一确定的?
未知量的个数?
方程的个数?
系数的个数与值?
表记未知量的符号?······
答案:系数的个数与值!!
对线性方程组的抽象→矩阵

- 矩阵的加减法——•对应位置元素做运算:

- 矩阵的标量乘法——每一个元素均乘以该常数:

- 矩阵的向量乘法——第一个矩阵的列数和第二个矩阵的行数相等:

要点:第一个矩阵M1大小:m×n,第二个矩阵M2大小:n×k,则M1与M2相乘得到的结果矩阵Mres的大小为: m×k
- 矩阵的转置:

- 矩阵(方阵)的逆:

概率&统计
• 平时不好好学习,考试的时候不确定能否及格
• 太阳一定是从东方升起的
• 我们绝对不可能先经历明天再经历昨天
• 赌徒有可能在赌场用一百美元赢到一千万美元
概率的数值范围:0≤P≤1
- P=0:不可能事件
- P=1:必然事件
- 0<P<1:随机事件 ⟸ 概率学关注的重点
抛硬币:
- 正面or反面
- 概率相等——1/2
- 每一次抛掷都是一次随机事件
抛硬币:
- 单次抛掷,正面朝上反面朝上概率都是1/2,那第一次第二次都出现正面朝上的概率如何计算?
答:这一事件由两个先后步骤组成:第一次抛掷和第二次抛掷事件的概率由两步骤各自的概率相乘得到:

Wait, 为什么事件的概率要由步骤的概率相乘得到?

总共四种情况,两次抛掷均为正面的情况只占一种,所以最终概率=1/4事件经由多个步骤完成,最终可能的结果种类是每一步可能结果数量相乘得到的。
联合概率
A事件(第一次抛掷正面朝上)发生的概率用P(A)表示
B事件(第二次抛掷正面朝上)发生的概率用P(B)表示
A和B同时发生的概率用P(AB)或P(A,B)表示
若A和B是相互独立的,则P(AB)=P(A)P(B)
若A和B不是相互独立的,则P(AB)=?
甲是普通人,抛硬币正面朝上的概率如前所述,乙是赌神,可通过小技巧使正面朝上的概率是0.7,那我们怎么描述让乙来抛硬币时正面朝上的概率?直接说P=0.7?

Why 同一事件(抛掷硬币正面朝上)对于不同的操作者而言,其对应的概率却不相同?
Key: 事件的先决条件不同
条件概率
- 在某个先决条件已发生的情况下,某一事件发生的概率
- 先决条件与讨论的事件是有关联的
- A为先决条件(操作者是赌神还是普通人),B为讨论的事件(抛掷硬币正面朝上),则当A已确定的情况下,B发生的概率表示为:P(B|A)
联合概率&条件概率的联系
若A和B是相互独立的,则P(AB)=P(A)P(B)
若A和B不是相互独立的,如何计算P(AB)?
Key: P(AB) = P(B|A)P(A)
情景:从赌神和普通人中随机选一个人抛硬币
P(A): 从两个人中选出赌神的概率,等于0.5
P(B|A): 选定赌神的情况下,他抛出正面朝上的概率,等于0.7
P(AB): 从两个人中选出赌神并抛出正面朝上的概率,等于0.35
第一次,第二次抛掷都是正面朝上,第三次抛掷还出现正面朝上的概率是1/2吗?
答:Key: 仍然是1/2,因为任意一次抛掷硬币与其它次之间都是独立的, 不相关的。
随机事件
- 在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件,简称事件。
- 抛硬币,正面朝上是一个随机事件
- 反面朝上亦是一个随机事件
- 掷骰子朝上的点数为偶数是一个随机事件
随机变量
- 一次随机试验可能出现的结果的数量化表示
- 一般用大写字母表示,如X, Y
- 抛掷两个骰子得到的向上的点数之和就是一个随机变量
- 连续型随机变量,如街访一个人,他/她的身高
- 离散型随机变量,如街访一个人,他/她的性别
数学期望
每种可能的结果乘上对应的概率再相加
- 期望的性质
1. E(C)=C,C为常数
2. E(CX)=CE(X),C为常数
3. E(X+Y)=E(X)+E(Y)
4. E(XY)=E(X)E(Y),当X, Y相互独立时
方差
度量随机变量和其数学期望之间的偏离程度


- 方差的性质
1. D(C)=0,C为常数
2. D(X+C)=D(X),C为常数
3. D(CX)=C^2 D(X),C为常数
4. D(X+Y)=D(X)+D(Y)+2Cov(X, Y)
5. D(X+Y)=D(X)+D(Y),当X和Y相互独立时
Cov(X, Y)=E{[X-E(X)][Y-E(Y)} : 协方差
标准差

(1)度量效果与方差一致
(2)方差的量纲和随机变量不一致
协方差
用于衡量两个变量的总体误差
协方差为正:两个变量的变化趋势相同,当一个大于其期望值时,另一个也大于,小于的情况亦然
协方差为负:两个变量的变化趋势相反,当一个大于其期望值时,另一个就小于,反之亦然
协方差为0:两个变量无线性相关性
两个变量独立,则协方差一定为0,但反之并不一定成立
- 公式

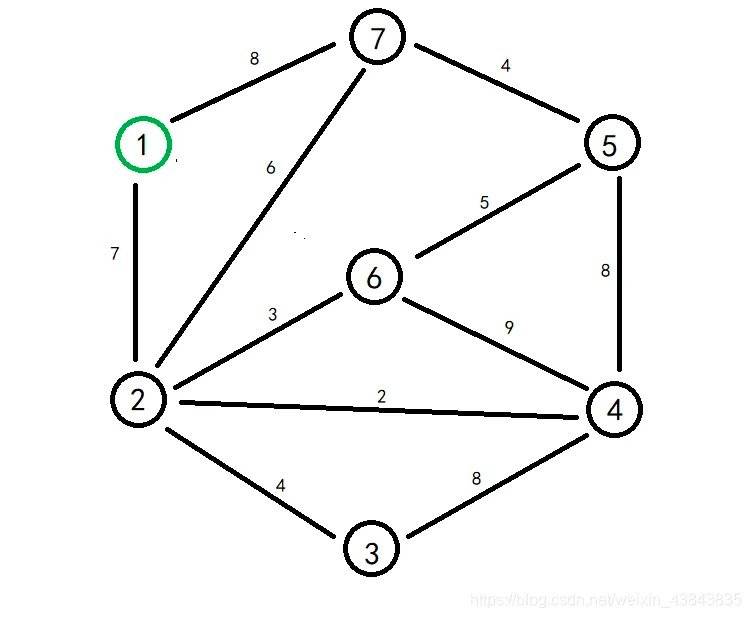
图论
什么是图?——由顶点和边构成的网络结构

为什么会有图论?——哥尼斯堡七桥问题(无解)

图的构成:顶点,边
有向图与无向图
图的同构
边的权重
环
与AI有什么关系?
最短路径搜索
推荐系统
社交网络分析
总结
数学如何运用于AI?
导数——反向传播, …
矩阵——AI模型的基本数据及参数结构, …
概率&统计——贝叶斯分类,最大似然估计, …
图论——概率图模型(贝叶斯网络,马尔可夫网络, …)
更多……